本文介绍几个理论固体物理常用的模型系统,并对其要素进行论证和检验。在构造模型哈密顿量时,可实践二次量子化。
固体当然是多体系统,
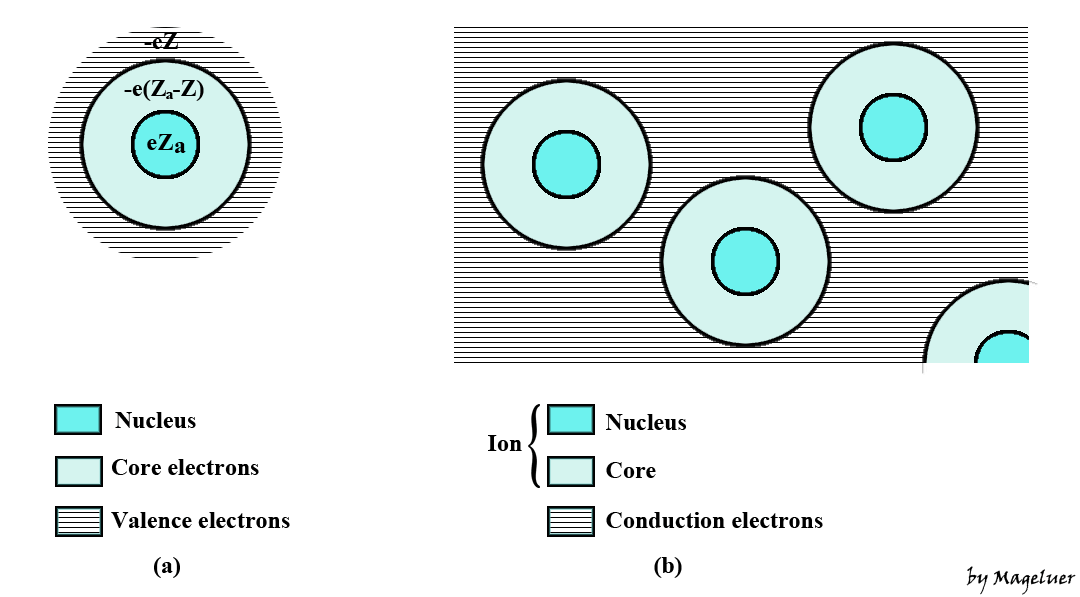
\[\text{Solid}=\sum_{i=1}^{N}\text{(particles)}_i\]由相互作用的原子或分子构成。每个粒子由一个或多个带正电的原子核和一个带负电的电子云组成。电子云可分为核心电子(core electrons)和价电子(valence electrons)(图 1)。核心电子紧紧束缚在原子核周围,通常占据封闭电子层——例外如稀土元素的$4f$层电子——对固体特性几乎没什么影响。价电子恰恰相反,它们占据非封闭壳层并负责成键构成固体。当然,核心电子和价电子之间的并非总是界限分明,这已是一种近似处理。在此意义上,晶格离子(lattice ion)指的是原子核与核心电子的结合体。由此得到以下模型:
固体:
一个由晶格离子和价电子组成的相互作用粒子系统。
相应的哈密顿量为:
\begin{equation} \label{eq:1} H=H_{\text{e}}+H_{\text{i}}+H_{\text{ei}} \end{equation}
电子子系统由算符$H_{\text{e}}$描述:
\begin{equation} \label{eq:2} H_{\text{e}}=\sum_{i=1}^{N_\text{e}}\frac{p_i^2}{2m}+\frac{1}{2}\frac{1}{4\pi\varepsilon_0}\sum_{i,j}^{i\neq j}\frac{e^2}{|\boldsymbol{r}_i-\boldsymbol{r}_j|}\equiv H_\text{e,kin}+H_\text{ee} \end{equation}
$N_\text{e}$是价电子数目。上式第一项表示动能,第二项是库伦相互作用。$\boldsymbol{r}_i$,$\boldsymbol{r}_j$是电子位置矢量。
离子子系统由算符$H_{\text{i}}$描述:
\begin{equation} \label{eq:3} H_{\text{i}}=\sum_{\alpha=1}^{N_\text{i}}\frac{p_\alpha^2}{2M_\alpha}+\frac{1}{2}\sum_{\alpha,\beta}^{\alpha\neq \beta}V_\text{i}(\boldsymbol{R}_\alpha-\boldsymbol{R}_\beta)\equiv H_\text{i,kin}+H_\text{ii} \end{equation}
离子-离子相互作用现在还不必明确写出,它总是成对作用,并对离子的平衡位置,$\boldsymbol{R}_\alpha^{(0)}$,构成严格的周期性晶格有所贡献。离子在平衡位置振荡,振荡能量是量子化的,基本量子叫做声子。方便起见,将$H_\text{ii}$分成:
\begin{equation} \label{eq:4} H_\text{ii}=H_\text{ii}^{(0)}+H_\text{p} \end{equation}
$H_\text{ii}^{(0)}$决定了固体的一些特性,例如固体中成键,而$H_\text{p}$则属于晶格动力学。
最后,两子系统间的相互作用是
\begin{equation} \label{eq:5} H_\text{ei}=\sum_{i=1}^{N_\text{e}}\sum_{\alpha=1}^{N_\text{i}}V_\text{ei}(\boldsymbol{r}_i-\boldsymbol{R}_\alpha) \end{equation}
方便起见,这里也做进一步分解:
\begin{equation} \label{eq:6} H_\text{ei}=H_\text{ei}^{(0)}+H_\text{e-p} \end{equation}
$H_\text{ei}^{(0)}$表示电子与处于平衡位置的离子间的相互作用而$H_\text{e-p}$表示电子-声子相互作用。
得到整个系统\eqref{eq:1}的精确解几乎不可能。可由以下三个步骤做个近似:
- 电子运动项,例如,在一个刚性的离子晶格中:$H_\text{e}+H_\text{ei}^{(0)}$。
- 离子运动项,例如,在均匀的电子气中:$H_\text{p}$。
- 耦合项,例如,用微扰理论处理:$H_\text{e-p}$。
接下来根据以上概念讨论电子子系统。
1 晶体电子
1.1 无相互作用Bloch电子
首先考虑刚性离子晶格中的电子,它们之间无相互作用,仅仅受周期性的晶格势影响,即如下哈密顿量:
\begin{equation} \label{eq:7} H_0=H_\text{e,kin}+H_\text{ei}^{(0)} \end{equation}
晶格势(lattice potential)来自处于平衡位置的离子:
\begin{equation} \label{eq:8} \widehat{V}(\boldsymbol{r}_i)=\sum_{\alpha=1}^{N_\text{i}}V_\text{ei}(\boldsymbol{r}_i-\boldsymbol{R}_\alpha^{(0)}) \end{equation}
更准确地说,离子的位置$\boldsymbol{R}_\alpha^{(0)}$为:
\begin{equation} \label{eq:9} \begin{split} \boldsymbol{R}_\alpha^{(0)}\Rightarrow\boldsymbol{R}_s^\boldsymbol{n}=\boldsymbol{R}^\boldsymbol{n}+\boldsymbol{R}_s\
\boldsymbol{n}=(n_1,n_2,n_3);\quad n_i\in\mathbb{Z} \end{split} \end{equation}
这里的$\boldsymbol{R}_s^\boldsymbol{n}$是Bravais格子:
\begin{equation} \label{eq:10} \boldsymbol{R}^\boldsymbol{n}=\sum_{i=1}^{3}n_i\boldsymbol{a}_i \end{equation}
$\boldsymbol{a}_1$,$\boldsymbol{a}_2$,$\boldsymbol{a}_3$是初基平移矢量,$\boldsymbol{R}_s$是初基原子的位置矢量。Bravais格子的周期性体现在:
\begin{equation} \label{eq:11} \widehat{V}(\boldsymbol{r}_i+\boldsymbol{R}^\boldsymbol{n})\overset{!}{=}\widehat{V}(\boldsymbol{r}_i) \end{equation}
$\widehat{V}(\boldsymbol{r}_i)=\widehat{V}(\hat{\boldsymbol{r}}_i)$是单粒子算符,可以代入
\begin{equation} \label{eq:12} H_\text{ei}^{(0)}=\sum_{i=1}^{N_\text{e}}\widehat{V}(\hat{\boldsymbol{r}}_i) \end{equation}
解如下本征值方程:
\begin{equation} \label{eq:13} h_0\psi_\boldsymbol{k}(\boldsymbol{r})=\varepsilon(\boldsymbol{k})\psi_\boldsymbol{k}(\boldsymbol{r}) \end{equation}
称$\psi_\boldsymbol{k}(\boldsymbol{r})$为Bloch函数而$\varepsilon(\boldsymbol{k})$为相应Bloch能。$\boldsymbol{k}$是第一布里渊区中的波矢,$h_0$表示算符:
\begin{equation} \label{eq:14} h_0=\frac{\boldsymbol{p}^2}{2m}+\widehat{V}(\hat{\boldsymbol{r}}) \end{equation}
方程\eqref{eq:13}的解并不简单。利用周期性条件\eqref{eq:11}可以导出基本的Bloch定理:
\begin{equation} \label{eq:15} \psi_\boldsymbol{k}(\boldsymbol{r}+\boldsymbol{R}^\boldsymbol{n})=e^{i\boldsymbol{k}\cdot\boldsymbol{R}^\boldsymbol{n}}\psi_\boldsymbol{k}(\boldsymbol{r}) \end{equation}
通常记作:
\begin{equation} \label{eq:16} \psi_\boldsymbol{k}(\boldsymbol{r})=u_\boldsymbol{k}(\boldsymbol{r})e^{i\boldsymbol{k}\cdot\boldsymbol{r}} \end{equation}
振幅函数必须满足Bravais格子的周期性:
\begin{equation} \label{eq:17} u_\boldsymbol{k}(\boldsymbol{r}+\boldsymbol{R}^\boldsymbol{n})=u_\boldsymbol{k}(\boldsymbol{r}) \end{equation}
Bloch函数$\psi_\boldsymbol{k}(\boldsymbol{r})$是正交完备的:
\begin{align} \label{eq:18} \int\mathrm{d}^3r\psi_\boldsymbol{k}^*(\boldsymbol{r})\psi_\boldsymbol{k’}(\boldsymbol{r})&=\delta_{\boldsymbol{k},\boldsymbol{k}’}\
\label{eq:19} \sum_\boldsymbol{k}^{\text{1.BZ}}\psi_\boldsymbol{k}^*(\boldsymbol{r})\psi_\boldsymbol{k}(\boldsymbol{r}’)&=\delta(\boldsymbol{r}-\boldsymbol{r}’) \end{align}
求和历遍第一布里渊区中的所有波矢$\boldsymbol{k}$,由于周期性边界条件,它们是离散的。$h_0$中不包含自旋部分,故其本征函数可分解为自旋和位形空间的函数:
\begin{align} \label{eq:20} \begin{split} |\boldsymbol{k}\sigma\rangle &\Longleftrightarrow \text{Bloch state}\
\langle\boldsymbol{r}|\boldsymbol{k}\sigma\rangle&=\psi_{\boldsymbol{k}\sigma}(\boldsymbol{r})=\psi_\boldsymbol{k}(\boldsymbol{r})\chi_\sigma\
\chi_\uparrow&=\begin{pmatrix}1\\0\end{pmatrix};\quad\chi_\downarrow=\begin{pmatrix}0\\1\end{pmatrix} \end{split} \end{align}
如果考虑来自不同能带的电子,Bloch函数将带有能带指标$n$。现在不考虑这些,下面的讨论仅限处于同一能带的电子。
定义:
\[a_{\boldsymbol{k}\sigma}^\dagger(a_{\boldsymbol{k}\sigma}):\quad\text{Bloch电子的产生(湮灭)算符}\]$H_0$是单体算符,由式(214)-二次量子化可得:
\[H_0=\sum_{\substack{\boldsymbol{k}\sigma\\\boldsymbol{k}'\sigma'}}\langle\boldsymbol{k}\sigma|h_0|\boldsymbol{k}'\sigma'\rangle a_{\boldsymbol{k}\sigma}^\dagger a_{\boldsymbol{k}'\sigma'}\]矩阵元可直接计算得到:
\begin{equation} \label{eq:21} \langle\boldsymbol{k}\sigma|h_0|\boldsymbol{k}’\sigma’\rangle=\varepsilon(\boldsymbol{k}’)\langle\boldsymbol{k}\sigma|\boldsymbol{k}’\sigma’\rangle=\varepsilon(\boldsymbol{k})\delta_{\boldsymbol{kk’}}\delta_{\sigma\sigma’} \end{equation}
上式中$|\boldsymbol{k}\sigma\rangle$是$h_0$本征函数。由此得到:
\begin{equation} \label{eq:22} H_0=\sum_{\boldsymbol{k}\sigma}\varepsilon(\boldsymbol{k})a_{\boldsymbol{k}\sigma}^\dagger a_{\boldsymbol{k}\sigma}=\sum_{\boldsymbol{k}\sigma}\varepsilon(\boldsymbol{k})n_{\boldsymbol{k}\sigma} \end{equation}
Bloch算符$a_{\boldsymbol{k}\sigma}$,$a_{\boldsymbol{k}\sigma}^\dagger$自然满足基本对易关系:
\begin{align} \label{eq:23} [a_{\boldsymbol{k}\sigma},a_{\boldsymbol{k}’\sigma’}]_+&=[a_{\boldsymbol{k}\sigma}^\dagger,a_{\boldsymbol{k}’\sigma’}^\dagger]_+=0\
\label{eq:24} [a_{\boldsymbol{k}\sigma},a_{\boldsymbol{k}’\sigma’}^\dagger]_+&=\delta_{\boldsymbol{kk’}}\delta_{\sigma\sigma’} \end{align}
如果忽略固体晶格结构而将离子晶格视作正电荷背景($\widehat{V}(\boldsymbol{r})=\text{const}$),Bloch函数将成为平面波,
\begin{equation} \label{eq:25} \psi_\boldsymbol{k}(\boldsymbol{r})\underset{[\widehat{V}(\boldsymbol{r})=\text{const}]}{\Rightarrow}\frac{1}{\sqrt{V}}e^{i\boldsymbol{k}\cdot\boldsymbol{r}} \end{equation}
相应Bloch能,由$p^2/2m=-(\hbar^2/2m)\Delta$:
\begin{equation} \label{eq:26} \varepsilon(\boldsymbol{k})\underset{[\widehat{V}(\boldsymbol{r})=\text{const}]}{\Rightarrow}\frac{\hbar^2k^2}{2m} \end{equation}
(这里$V$是固体的体积,要注意区分$V$和晶格势$\widehat{V}$!)接着讨论两种颇具应用性的两种其他表象,比如
场算符(field operators):
\[\widehat{\psi}\_\sigma^\dagger(\boldsymbol{r}),\widehat{\psi}\_\sigma(\boldsymbol{r})\]
可由式(165)—式(175)-二次量子化进行理解,只不过加入了电子自旋,其对易关系也可按二次量子化中进行推广,例如:
\begin{equation} \label{eq:27} [\widehat{\psi}_\sigma(\boldsymbol{r}),\widehat{\psi}_{\sigma’}^\dagger(\boldsymbol{r}’)]_+=\delta(\boldsymbol{r}-\boldsymbol{r}’)\delta_{\sigma\sigma’} \end{equation}
由此得到$H_0$:
\begin{align} \label{eq:28} \begin{split} H_0&=\sum_{\sigma,\sigma’}\iint\mathrm{d}^3r\,\mathrm{d}^3r’\langle\boldsymbol{r}\sigma|h_0|\boldsymbol{r}’\sigma’\rangle\widehat{\psi}_\sigma^\dagger(\boldsymbol{r})\widehat{\psi}_{\sigma’}(\boldsymbol{r}’)=\
&=\sum_{\sigma,\sigma’}\iint\mathrm{d}^3r\,\mathrm{d}^3r’\delta_{\sigma\sigma’}\left(-\frac{\hbar^2}{2m}\Delta_{\boldsymbol{r}’}+\widehat{V}(\boldsymbol{r}’)\right)\delta(\boldsymbol{r}-\boldsymbol{r}’)\widehat{\psi}_\sigma^\dagger(\boldsymbol{r})\widehat{\psi}_{\sigma’}(\boldsymbol{r}’)=\
&=\sum_{\sigma}\int\mathrm{d}^3r\widehat{\psi}_\sigma^\dagger(\boldsymbol{r})\left(-\frac{\hbar^2}{2m}\Delta_{\boldsymbol{r}}+\widehat{V}(\boldsymbol{r})\right)\widehat{\psi}_\sigma(\boldsymbol{r}) \end{split} \end{align}
此外,一个常用的特殊表象利用了
Wannier函数:
\begin{equation} \label{eq:29} \omega(\boldsymbol{r}-\boldsymbol{R}_i)=\frac{1}{\sqrt{N_\text{i}}}\sum_{\boldsymbol{k}}^{\text{1.BZ}}e^{-i\boldsymbol{k}\cdot\boldsymbol{R}_i}\psi_{\boldsymbol{k}\sigma}(\boldsymbol{r}) \end{equation}
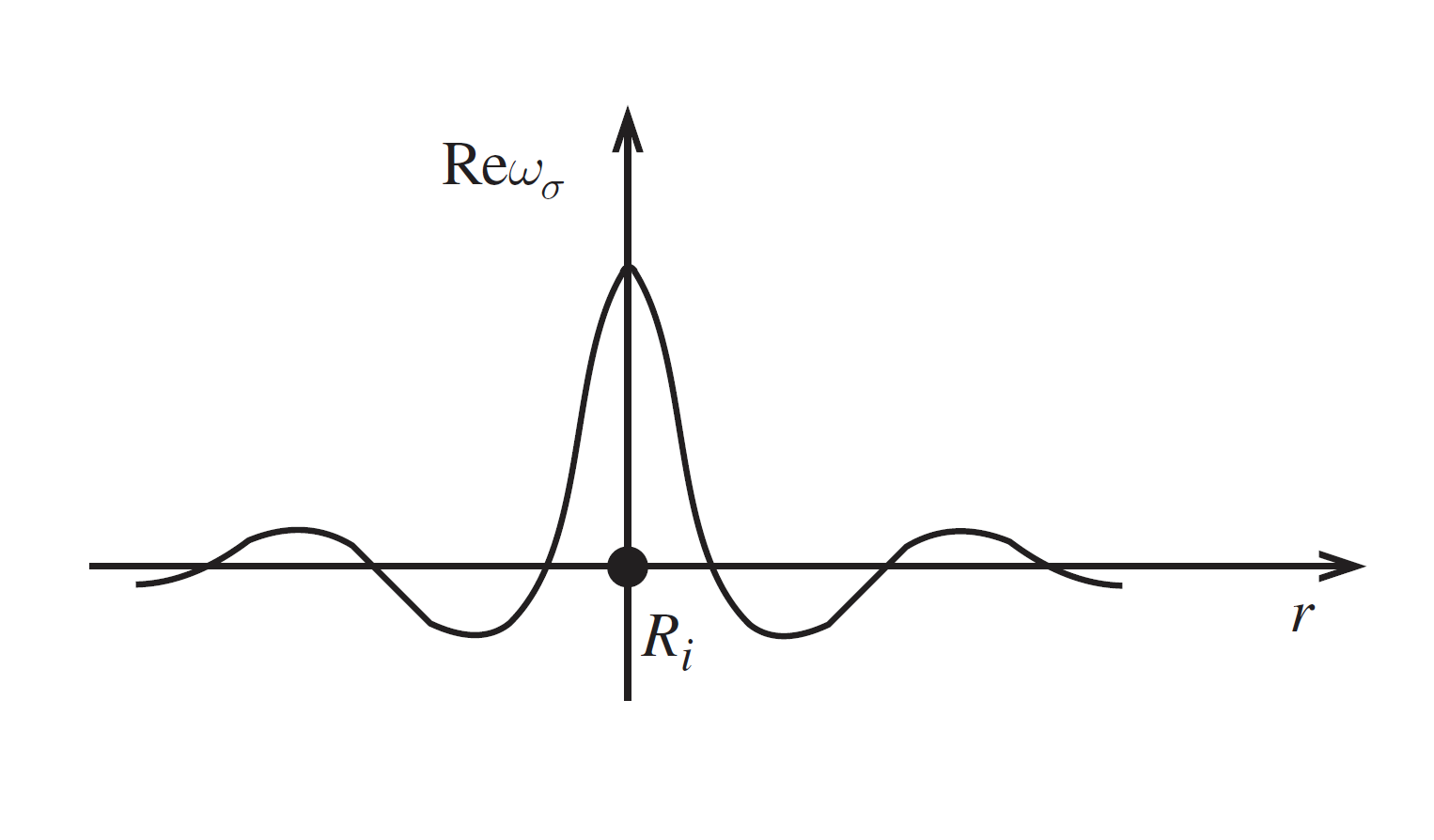
此函数的一个典型特征是在格点$R_\text{i}$处高度局域化(图 2)。由式\eqref{eq:18}及
\begin{equation} \label{eq:30} \frac{1}{N_\text{i}}\sum_{\boldsymbol{k}}^{\text{1.BZ}}e^{-i\boldsymbol{k}\cdot(\boldsymbol{R}_i-\boldsymbol{R}_j)}=\delta_{ij} \end{equation}
可以证明其正交关系:
\begin{equation} \label{eq:31} \int\mathrm{d}^3r\omega_\sigma^*(\boldsymbol{r}-\boldsymbol{R}_i)\omega_\sigma^*(\boldsymbol{r}-\boldsymbol{R}_j)=\delta_{\sigma\sigma’}\delta_{ij} \end{equation}
采用如下记号:
\begin{align} \label{eq:32} \begin{split} |i\sigma\rangle&\Longleftrightarrow\text{Wannier state}\
\langle\boldsymbol{r}|i\sigma\rangle&=\omega_\sigma(\boldsymbol{r}-\boldsymbol{R_i})\
a_{i\sigma}^\dagger(a_{i\sigma}):&\text{格矢}\boldsymbol{R}_i\text{处电子Wannier态的产生(湮灭)算符} \end{split} \end{align}
$H_0$的二次量子化形式为:
\begin{equation} \label{eq:33} H_0=\sum_{ij\sigma}T_{ij}a_{i\sigma}^\dagger a_{j\sigma} \end{equation}
其物理图像相当清晰:处于$\boldsymbol{R}_j$处(于此湮灭)自旋为$\sigma$的电子跃迁到格点$\boldsymbol{R}_i$(于此产生)。故$T_{ij}$被称作
"跃迁"积分
下面开始具体计算:
\begin{align} \begin{split} \langle i\sigma|h_0|j\sigma’\rangle&=\delta_{\sigma\sigma’}\langle i\sigma|h_0|j\sigma\rangle=\
&=\delta_{\sigma\sigma’}\sum_{\substack{\boldsymbol{k},\boldsymbol{k}’\
\sigma_1,\sigma_2}}\langle i\sigma|\boldsymbol{k}\sigma_1\rangle\langle\boldsymbol{k}\sigma_1|h_0|\boldsymbol{k}’\sigma_2\rangle\langle\boldsymbol{k}’\sigma_2|j\sigma\rangle=\
&=\delta_{\sigma\sigma’}\sum_{\substack{\boldsymbol{k},\boldsymbol{k}’\
\sigma_1,\sigma_2}}\varepsilon(\boldsymbol{k}’)\langle i\sigma|\boldsymbol{k}\sigma_1\rangle\langle\boldsymbol{k}\sigma_1|\boldsymbol{k}’\sigma_2\rangle\langle\boldsymbol{k}’\sigma_2|j\sigma\rangle=\
&=\delta_{\sigma\sigma’}\sum_{\boldsymbol{k},\sigma_1}\varepsilon(\boldsymbol{k})\langle i\sigma|\boldsymbol{k}\sigma_1\rangle\langle\boldsymbol{k}\sigma_1|j\sigma\rangle \end{split} \label{eq:34} \end{align}
剩余矩阵元作如下计算:
\begin{align} \label{eq:35} \begin{split} \langle i\sigma|\boldsymbol{k}\sigma_1\rangle&=\int\mathrm{d}^3\langle i\sigma|\boldsymbol{r}\rangle\langle\boldsymbol{r}|\boldsymbol{k}\sigma_1\rangle=\
&=\int\mathrm{d}^3\omega_\sigma^*(\boldsymbol{r}-\boldsymbol{R}_i)\psi_{\boldsymbol{k}\sigma_1}(\boldsymbol{r})=\
&=\frac{1}{\sqrt{N_\text{i}}}\sum_{\boldsymbol{k}’}e^{i\boldsymbol{k}\cdot\boldsymbol{R}_i}\int\mathrm{d}^3r\psi_{\boldsymbol{k}’\sigma}^*(\boldsymbol{r})\psi_{\boldsymbol{k}\sigma_1}(\boldsymbol{r})=\
&=\frac{1}{\sqrt{N_\text{i}}}\sum_{\boldsymbol{k}’}e^{i\boldsymbol{k}\cdot\boldsymbol{R}_i}\delta_{\boldsymbol{kk}’}\delta_{\sigma\sigma_1}=\delta_{\sigma\sigma_1}\frac{e^{i\boldsymbol{k}\cdot\boldsymbol{R}_i}}{\sqrt{N_\text{i}}} \end{split} \end{align}
上式第三行用到式\eqref{eq:29},由此得到式\eqref{eq:34}:
\begin{equation} \label{eq:36} \langle i\sigma|h_0|j\sigma’\rangle=\delta_{\sigma\sigma’}T_{ij} \end{equation}
相应的:
\begin{equation} \label{eq:37} T_{ij}=\sum_{\boldsymbol{k},\sigma_1}\varepsilon(\boldsymbol{k})\delta_{\sigma\sigma_1}\frac{e^{i\boldsymbol{k}\cdot\boldsymbol{R}_i}}{\sqrt{N_\text{i}}}\delta_{\sigma\sigma_1}\frac{e^{-i\boldsymbol{k}\cdot\boldsymbol{R}_j}}{\sqrt{N_\text{i}}}=\frac{1}{N_\text{i}}\sum_\boldsymbol{k}\varepsilon(\boldsymbol{k})e^{i\boldsymbol{k}\cdot(\boldsymbol{R}_i-\boldsymbol{R}_j)} \end{equation}
其逆为:
\begin{equation} \label{eq:38} \varepsilon(\boldsymbol{k})=\frac{1}{N_\text{i}}\sum_{i,j}T_{ij}e^{-i\boldsymbol{k}\cdot(\boldsymbol{R}_i-\boldsymbol{R}_j)} \end{equation}
代入式\eqref{eq:37}再结合式\eqref{eq:30}易验证:
\[ \begin{split} &\frac{1}{N_\text{i}}\sum_\boldsymbol{k}\varepsilon(\boldsymbol{k})e^{i\boldsymbol{k}\cdot(\boldsymbol{R}_i-\boldsymbol{R}_j)}=\
=&\frac{1}{N_\text{i}}\sum_\boldsymbol{k}\left(\frac{1}{N_\text{i}}\sum_{i’,j’}T_{i’j’}e^{-i\boldsymbol{k}\cdot(\boldsymbol{R}_{i’}-\boldsymbol{R}_{j’})}\right)e^{i\boldsymbol{k}\cdot(\boldsymbol{R}_i-\boldsymbol{R}_j)}=\
=&\sum_{i’,j’}T_{i’j’}\sum_\boldsymbol{k}\left(\frac{1}{N_\text{i}}e^{i\boldsymbol{k}\cdot(\boldsymbol{R}_{i}-\boldsymbol{R}_{i’})}\right)\left(\frac{1}{N_\text{i}}e^{i\boldsymbol{k}\cdot(\boldsymbol{R}_{j’}-\boldsymbol{R}_{j})}\right)=\
=&\sum_{i’,j’}T_{i’j’}\delta_{ii’}\delta_{jj’}=\
=&T_{ij} \end{split} \]
Bloch算符和Wannier算符之间的关系可仿照式(171)-二次量子化得到:
\begin{align} \label{eq:39} a_{i\sigma}=\frac{1}{\sqrt{N_\text{i}}}\sum_{\boldsymbol{k}}^{\text{1.BZ}}e^{i\boldsymbol{k}\cdot\boldsymbol{R}_i}a_{\boldsymbol{k}\sigma}\
a_{\boldsymbol{k}\sigma}=\frac{1}{\sqrt{N_\text{i}}}\sum_{i=1}^{N_\text{i}}e^{-i\boldsymbol{k}\cdot\boldsymbol{R}_i}a_{i\sigma}\
\end{align}
由Bloch算符的对易关系\eqref{eq:23},\eqref{eq:24}可得到Wannier算符的对易关系: \begin{align} \label{eq:41} [a_{i\sigma},a_{j\sigma’}]_+&=[a_{i\sigma}^\dagger,a_{j\sigma’}^\dagger]_+=0\
\label{eq:42} [a_{i\sigma},a_{j\sigma’}^\dagger]_+&=\delta_{ij}\delta_{\sigma\sigma’} \end{align}
1.2 凝胶模型
此模型足以描述简单金属,且基于如下假设:
- 处于体积$V=L^3$中的$N_\text{e}$个电子之间为库伦相互作用:
\begin{equation} \label{eq:43} H_\text{ee}=\frac{e^2}{8\pi\varepsilon_0}\sum_{i,j}^{i\neq j}\frac{1}{|\boldsymbol{r}_i-\boldsymbol{r}_j|} \end{equation} - 离子仅带一个正电荷:
\begin{equation} \label{eq:44} N_\text{e}=N_\text{i}=N \end{equation} - 离子形成均匀的背景场并保证:(a)体系电荷中性;(b)晶格势为常值。
此时Bloch函数为平面波形式:
\begin{equation} \label{eq:45} \psi_{\boldsymbol{k}\sigma}(\boldsymbol{r})\Rightarrow\frac{1}{\sqrt{V}}e^{i\boldsymbol{k}\cdot\boldsymbol{r}}\chi_\sigma \end{equation} - 周期性边界条件导致波矢离散化:
\begin{equation} \label{eq:46} \boldsymbol{k}=\frac{2\pi}{L}(n_x,n_y,n_z),\quad n_{x,y,z}\in\boldsymbol{Z} \end{equation}
符合这些假设的模型哈密顿的一次量子化形式是什么样?它应包含如下三项:
\begin{equation} \label{eq:47} H=H_\text{e}+H_++H_\text{e+} \end{equation}
$H_\text{e}$是关键项,其意义见式\eqref{eq:2}。$H_+$表示均匀分布的离子电荷,均匀分布的意思是离子的电荷密度$n(\boldsymbol{r})$与位置无关:
\begin{equation} \label{eq:48} n(\boldsymbol{r})\Rightarrow\frac{N}{V} \end{equation}
$H_+$项为: \begin{equation} \label{eq:49} H_+=\frac{e^2}{8\pi\varepsilon_0}\iint\mathrm{d}^3r\,\mathrm{d}^3r’\frac{n(\boldsymbol{r})\cdot n(\boldsymbol{r’})}{|\boldsymbol{r}-\boldsymbol{r’}|}e^{-\alpha|\boldsymbol{r}-\boldsymbol{r’}|} \end{equation}
基于第4个假设,我们的结果应在热力学极限下讨论,即$N\to\infty,V\to\infty,N/V\to\text{const}$。由于库仑力长程有效,积分会发散,于是加上一个收敛因子$\exp(-\alpha|\boldsymbol{r}-\boldsymbol{r’}|)$,$\alpha>0$。积分完成后再令$\alpha\to0$。
结合\eqref{eq:48}可得:
\[ \begin{split} &\iint\mathrm{d}^3r\,\mathrm{d}^3r’\frac{e^{-\alpha|\boldsymbol{r}-\boldsymbol{r’}|}}{|\boldsymbol{r}-\boldsymbol{r’}|}=\
=&\iint\mathrm{d}^3r\,\mathrm{d}^3r’\frac{e^{-\alpha r}}{r}=\qquad(\boldsymbol{r}-\boldsymbol{r’}\to\boldsymbol{r},\boldsymbol{r’}\to\boldsymbol{r’})\
=&V\int_V\mathrm{d}^3r\frac{e^{-\alpha r}}{r}=\
=&V\int_0^\infty\mathrm{d}r4\pi re^{-\alpha r}=\
=&\frac{4\pi V}{\alpha^2} \end{split} \]
上式用到了:
\[ \begin{split} &\int_0^\infty\mathrm{d}x\,\, x^ne^{-\alpha x}=\
=&\int_0^\infty\mathrm{d}x\,\,(-1)^n\frac{\mathrm{d}^n}{\mathrm{d}\alpha^n}e^{-\alpha x}=\
=&(-1)^n\frac{\mathrm{d}^n}{\mathrm{d}\alpha^n}\int_0^\infty\mathrm{d}x\,\, e^{-\alpha x}=\
=&(-1)^n\frac{\mathrm{d}^n}{\mathrm{d}\alpha^n}\frac{1}{\alpha}=\
=&(-1)^n\frac{(-1)^n}{\alpha^{n+1}}=\
=&\frac{1}{\alpha^{n+1}} \end{split} \]
其中$n\in\boldsymbol{N}$,由此得到:
\begin{equation} \label{eq:50} H_+=\frac{e^2}{8\pi\varepsilon_0}\frac{\widehat{N}^2}{V}\frac{4\pi}{\alpha^2} \end{equation}
可见,当$\alpha\to0$时$H_+$确实发散,但它会和其他项抵消掉。\eqref{eq:47}中的$H_\text{e+}$表示电子和均匀离子背景之间的作用:
\begin{equation} \label{eq:51} H_\text{e+}=-\frac{e^2}{4\pi\varepsilon_0}\sum_{i=1}^{N}\int\mathrm{d}^3r\frac{n(\boldsymbol{r})}{|\boldsymbol{r}-\boldsymbol{r}_i|}e^{-\alpha|\boldsymbol{r}-\boldsymbol{r}_i|} \end{equation}
和计算$H_+$一样,得到:
\[ \begin{split} H_\text{e+}=&-\frac{e^2}{4\pi\varepsilon_0}\frac{N}{V}\sum_{i=1}^{N}\int\mathrm{d}^3r\frac{e^{-\alpha|\boldsymbol{r}-\boldsymbol{r}_i|}}{|\boldsymbol{r}-\boldsymbol{r}_i|}=\
=&-\frac{e^2}{4\pi\varepsilon_0}\frac{N}{V}\sum_{i=1}^{N}\frac{4\pi}{\alpha^2} \end{split} \]
把粒子数$N$替换为粒子数算符$\widehat{N}$得到:
\begin{equation} \label{eq:52} H_\text{e+}=-\frac{e^2}{4\pi\varepsilon_0}\frac{\widehat{N}^2}{V}\frac{4\pi}{\alpha^2} \end{equation}
合起来就是:
\begin{equation} \label{eq:53} H=H_\text{e}-\frac{1}{2}\frac{e^2}{4\pi\varepsilon_0}\frac{\widehat{N}^2}{V}\frac{4\pi}{\alpha^2} \end{equation}
当$\alpha\to0$时依然发散,但我们将看到,$H_\text{e}$中正好有一项能和上式第二项抵消。事实上,$H_\text{e}$是最关键的算符,根据\eqref{eq:2},其包含动能项$H_0$\eqref{eq:7}和库伦作用项$H_\text{ee}$\eqref{eq:43}。$H_0$已经在前面完成二次量子化了。$H_\text{ee}$是个典型的两体算符,根据式(214)-二次量子化,其在Bloch表象中为:
\begin{equation} \label{eq:54} H_\text{ee}=\frac{1}{2}\sum_{\substack{\boldsymbol{k}_1\cdots\boldsymbol{k}_4\\ \sigma_1\cdots\sigma_4}}v(\boldsymbol{k}_1\sigma_1,\ldots,\boldsymbol{k}_4\sigma_4)a_{\boldsymbol{k}_1\sigma_1}^\dagger a_{\boldsymbol{k}_2\sigma_2}^\dagger a_{\boldsymbol{k}_4\sigma_4}a_{\boldsymbol{k}_3\sigma_3} \end{equation}
矩阵元
\[ \begin{split} &v(\boldsymbol{k}_1\sigma_1,\ldots,\boldsymbol{k}_4\sigma_4)=\
=&\frac{e^2}{4\pi\varepsilon_0}\left\langle(\boldsymbol{k}_1\sigma_1)^{(1)}(\boldsymbol{k}_2\sigma_2)^{(2)}\left|\frac{1}{|\hat{\boldsymbol{r}}^{(1)}-\hat{\boldsymbol{r}}^{(2)}|}\right|(\boldsymbol{k}_3\sigma_3)^{(1)}(\boldsymbol{k}_4\sigma_4)^{(2)}\right\rangle \end{split} \]
只有在$\sigma_1=\sigma_3$和$\sigma_2=\sigma_4$才不为零,由于算符本身与自旋无关:
\[ \begin{split} v(\boldsymbol{k}_1\sigma_1,\ldots,\boldsymbol{k}_4\sigma_4)&=\frac{e^2}{4\pi\varepsilon_0}\iint\mathrm{d}^3r_1\,\mathrm{d}^3r_2\Big\langle\boldsymbol{k}_1^{(1)}\boldsymbol{k}_2^{(2)}\Big|\frac{1}{|\hat{\boldsymbol{r}}^{(1)}-\hat{\boldsymbol{r}}^{(2)}|}\cdot\
&\cdot\Big|\boldsymbol{r}_1^{(1)}\boldsymbol{r}_2^{(2)}\Big\rangle\Big\langle\boldsymbol{r}_1^{(1)}\boldsymbol{r}_2^{(2)}\Big|\boldsymbol{k}_3^{(1)}\boldsymbol{k}_4^{(2)}\Big\rangle\delta_{\sigma_1\sigma_2}\delta_{\sigma_3\sigma_4}=\
&=\frac{e^2}{4\pi\varepsilon_0}\iint\mathrm{d}^3r_1\,\mathrm{d}^3r_2\frac{1}{|\boldsymbol{r}_1-\boldsymbol{r}_2|}\Big\langle\boldsymbol{k}_1^{(1)}\boldsymbol{k}_2^{(2)}\Big|\boldsymbol{r}_1^{(1)}\boldsymbol{r}_2^{(2)}\Big\rangle\cdot\
&\cdot\Big\langle\boldsymbol{r}_1^{(1)}\boldsymbol{r}_2^{(2)}\Big|\boldsymbol{k}_3^{(1)}\boldsymbol{k}_4^{(2)}\Big\rangle\delta_{\sigma_1\sigma_2}\delta_{\sigma_3\sigma_4}=\
&=\frac{e^2}{4\pi\varepsilon_0}\iint\mathrm{d}^3r_1\,\mathrm{d}^3r_2\frac{1}{|\boldsymbol{r}_1-\boldsymbol{r}_2|}\psi_{\boldsymbol{k}_1}^*(\boldsymbol{r}_1)\psi_{\boldsymbol{k}_2}^*(\boldsymbol{r}_2)\cdot\
&\cdot\psi_{\boldsymbol{k}_3}(\boldsymbol{r}_1)\psi_{\boldsymbol{k}_4}(\boldsymbol{r}_2)\delta_{\sigma_1\sigma_2}\delta_{\sigma_3\sigma_4} \end{split} \]
利用Bloch定理\eqref{eq:15},可进一步发现:
\[ \boldsymbol{k}_1+\boldsymbol{k}_2=\boldsymbol{k}_3+\boldsymbol{k}_4 \]
这只需通过简单的变量替换便能看到。于是得到:
\begin{align} \label{eq:55} \begin{split} v(\boldsymbol{k}_1\sigma_1,\ldots,\boldsymbol{k}_4\sigma_4)=&\delta_{\sigma_1\sigma_2}\delta_{\sigma_3\sigma_4}\delta_{\boldsymbol{k}_1+\boldsymbol{k}_2,\boldsymbol{k}_3+\boldsymbol{k}_4}v(\boldsymbol{k}_1,\ldots,\boldsymbol{k}_4),\
v(\boldsymbol{k}_1,\ldots,\boldsymbol{k}_4)=&\frac{e^2}{4\pi\varepsilon_0}\iint\mathrm{d}^3r_1\,\mathrm{d}^3r_2\psi_{\boldsymbol{k}_1}^*(\boldsymbol{r}_1)\psi_{\boldsymbol{k}_2}^*(\boldsymbol{r}_2)\cdot\
&\cdot\frac{1}{|\boldsymbol{r}_1-\boldsymbol{r}_2|}\psi_{\boldsymbol{k}_3}(\boldsymbol{r}_1)\psi_{\boldsymbol{k}_4}(\boldsymbol{r}_2) \end{split} \end{align}
对库伦作用项$H_\text{ee}$,便得到如下表达式:
\begin{equation} \label{eq:56} H_\text{ee}=\frac{1}{2}\sum_{\substack{\boldsymbol{k}_1,\ldots,\boldsymbol{k}_4\\ \sigma,\sigma’}}v(\boldsymbol{k}_1,\ldots,\boldsymbol{k}_4)\delta_{\boldsymbol{k}_1+\boldsymbol{k}_2,\boldsymbol{k}_3+\boldsymbol{k}_4}a_{\boldsymbol{k}_1\sigma}^\dagger a_{\boldsymbol{k}_2\sigma’}^\dagger a_{\boldsymbol{k}_4\sigma’}a_{\boldsymbol{k}_3\sigma} \end{equation}
在凝胶模型中,$\psi_{\boldsymbol{k}}(\boldsymbol{r})$是平面波,所以作如下计算:
\begin{align} \label{eq:57} \begin{split} &v_\alpha(\boldsymbol{k}_1,\ldots,\boldsymbol{k}_4)=\
=&\frac{e^2}{4\pi\varepsilon_0}\frac{1}{V^2}\iint\mathrm{d}^3r_1\,\mathrm{d}^3r_2\frac{e^{-i(\boldsymbol{k}_1-\boldsymbol{k}_3)\cdot\boldsymbol{r}_1}e^{-i(\boldsymbol{k}_2-\boldsymbol{k}_4)\cdot\boldsymbol{r}_2}}{|\boldsymbol{r}_1-\boldsymbol{r}_2|}e^{-\alpha|\boldsymbol{r}_1-\boldsymbol{r}_2|} \end{split} \end{align}
令
\begin{align} \label{eq:58} \begin{split} &\boldsymbol{r}=\boldsymbol{r}_1-\boldsymbol{r}_2;\qquad&\boldsymbol{R}=\frac{1}{2}(\boldsymbol{r}_1+\boldsymbol{r}_2)\
\Longleftrightarrow&\boldsymbol{r}_1=\frac{1}{2}\boldsymbol{r}+\boldsymbol{R};\qquad&\boldsymbol{r}_2=-\frac{1}{2}\boldsymbol{r}+\boldsymbol{R} \end{split} \end{align}
雅可比行列式为$1$,接着计算:
\[ \begin{split} v_\alpha(\boldsymbol{k}_1,\ldots,\boldsymbol{k}_4)=&\frac{e^2}{4\pi\varepsilon_0}\frac{1}{V}\int\mathrm{d}^3R\,e^{-i(\boldsymbol{k}_1-\boldsymbol{k}_3+\boldsymbol{k}_2-\boldsymbol{k}_4)\cdot\boldsymbol{R}}\cdot\
&\cdot\frac{1}{V}\int\mathrm{d}^3r\,\frac{1}{r}e^{-\alpha r}e^{-(i/2)(\boldsymbol{k}_1-\boldsymbol{k}_3-\boldsymbol{k}_2+\boldsymbol{k}_4)\cdot\boldsymbol{r}}=\
=&\frac{e^2}{4\pi\varepsilon_0}\delta_{\boldsymbol{k}_1+\boldsymbol{k}_2,\boldsymbol{k}_3+\boldsymbol{k}_4}\frac{1}{V}\int\mathrm{d}^3r\,\frac{e^{-i(\boldsymbol{k}_1-\boldsymbol{k}_3)\cdot\boldsymbol{r}}e^{-\alpha r}}{r} \end{split} \]
利用
\begin{align} \label{eq:59} \begin{split} \int\mathrm{d}^3r\,\frac{e^{-i\boldsymbol{q}\cdot\boldsymbol{r}}}{r}e^{-\alpha r}&=\int_0^{2\pi}\mathrm{d}\phi\int_0^\infty\mathrm{d}r\int_0^\pi\mathrm{d}\theta\,r^2\sin\theta\frac{e^{iqr\cos\theta}}{r}e^{-\alpha r}=\
&=2\pi\int_0^\infty\mathrm{d}r\int_0^\pi\mathrm{d}(\cos\theta)\left(-re^{iqr\cos\theta}e^{-\alpha r}\right)=\
&=2\pi\int_0^\infty\mathrm{d}r\left[\frac{e^{iqr\cos\theta}}{-iq}\right]_0^\pi e^{-\alpha r}=\
&=2\pi\int_0^\infty\mathrm{d}r\frac{-1}{iq}\left(e^{-(\alpha+iq)r}-e^{-(\alpha-iq)r}\right)=\
&=2\pi\frac{-1}{iq}\left(\frac{1}{\alpha+iq}-\frac{1}{\alpha-iq}\right)=\
&=\frac{4\pi}{q^2+\alpha^2} \end{split} \end{align}
上式在极坐标中将$\boldsymbol{q}$固定于$z$轴。最终得到:
\begin{equation} \label{eq:60} v_\alpha(\boldsymbol{k}_1,\ldots,\boldsymbol{k}_4)=\frac{e^2}{\varepsilon_0V[(\boldsymbol{k}_1-\boldsymbol{k}_3)^2+\alpha^2]}\delta_{\boldsymbol{k}_1-\boldsymbol{k}_3,\boldsymbol{k}_4-\boldsymbol{k}_2} \end{equation}
代入\eqref{eq:56}得到:
\begin{gather} \label{eq:61} H_\text{ee}^{(\alpha)}=\frac{1}{2}\sum_{\substack{\boldsymbol{k},\boldsymbol{p},\boldsymbol{q}\\ \sigma,\sigma’}}v_\alpha(\boldsymbol{q})a_{\boldsymbol{k}+\boldsymbol{q}\sigma}^\dagger a_{\boldsymbol{p}-\boldsymbol{q}\sigma’}^\dagger a_{\boldsymbol{p}\sigma’}a_{\boldsymbol{k}\sigma},\
\label{eq:62} v_\alpha(\boldsymbol{q})=\frac{e^2}{\varepsilon_0V(q^2+\alpha^2)} \end{gather}
考虑库伦作用中$q=0$的项:
\begin{align} \begin{split} &\frac{1}{2}\frac{e^2}{\varepsilon_0V\alpha^2}\sum_{\substack{\boldsymbol{k},\boldsymbol{p}\\ \sigma,\sigma’}}a_{\boldsymbol{k}\sigma}^\dagger a_{\boldsymbol{p}\sigma’}^\dagger a_{\boldsymbol{p}\sigma’}a_{\boldsymbol{k}\sigma}=\
&=\frac{1}{2}\frac{e^2}{\varepsilon_0V\alpha^2}\sum_{\substack{\boldsymbol{k},\boldsymbol{p}\\ \sigma,\sigma’}}a_{\boldsymbol{p}\sigma’}^\dagger\left(-a_{\boldsymbol{k}\sigma}^\dagger a_{\boldsymbol{p}\sigma’}\right)a_{\boldsymbol{k}\sigma}=\
&=\frac{1}{2}\frac{e^2}{\varepsilon_0V\alpha^2}\sum_{\substack{\boldsymbol{k},\boldsymbol{p}\\ \sigma,\sigma’}}a_{\boldsymbol{p}\sigma’}^\dagger\left(-\delta_{\sigma\sigma’}\delta_{\boldsymbol{k}\boldsymbol{p}}+a_{\boldsymbol{p}\sigma’}a_{\boldsymbol{k}\sigma}^\dagger\right)a_{\boldsymbol{k}\sigma}=\
&=\frac{1}{2}\frac{e^2}{\varepsilon_0V\alpha^2}\sum_{\substack{\boldsymbol{k},\boldsymbol{p}\\ \sigma,\sigma’}}\left(-\delta_{\sigma\sigma’}\delta_{\boldsymbol{k}\boldsymbol{p}}n_{\boldsymbol{k}\sigma}+n_{\boldsymbol{p}\sigma’}n_{\boldsymbol{k}\sigma}\right)=\
&=\frac{e^2}{2\varepsilon_0V\alpha^2}\left[-\widehat{N}+(\widehat{N})^2\right] \end{split} \label{eq:63} \end{align}
上式利用了Bloch算符的基本对易关系。可见\eqref{eq:63}的第2项与\eqref{eq:53}相抵消,即$H_+$的贡献被$H_\text{e+}$消除了。当将能量平均到每个粒子时\eqref{eq:63}的第1项在热力学极限下也消失了:
\[ -\frac{e^2}{2\varepsilon_0V\alpha^2}\xrightarrow[N\to\infty;V\to\infty]{}0 \]
所以一开始就可以丢掉。最后取极限$\alpha\to0$,得到
凝胶模型哈密顿量:
\begin{equation} \label{eq:64} H=\sum_{\boldsymbol{k}\sigma}\varepsilon_0(\boldsymbol{k})a_{\boldsymbol{k}\sigma}^\dagger a_{\boldsymbol{k}\sigma}+\frac{1}{2}\sum_{\substack{\boldsymbol{k},\boldsymbol{p},\boldsymbol{q}\\ \sigma,\sigma’}}^{q\neq0}v_0(\boldsymbol{q})a_{\boldsymbol{k}+\boldsymbol{q}\sigma}^\dagger a_{\boldsymbol{p}-\boldsymbol{q}\sigma’}^\dagger a_{\boldsymbol{p}\sigma’}a_{\boldsymbol{k}\sigma} \end{equation}
从\eqref{eq:26}可见
\begin{equation} \label{eq:65} \varepsilon_0(\boldsymbol{k})=\frac{\hbar^2k^2}{2m} \end{equation}
为动能的矩阵元,而
\begin{equation} \label{eq:66} v_0(\boldsymbol{q})=\frac{1}{V}\frac{e^2}{\varepsilon_0q^2} \end{equation}
属于库伦作用。
除此之外,再导出一种$H$的常用表示,用到了
电子密度算符:
\begin{equation} \label{eq:67} \hat{\rho}(\boldsymbol{r})=\sum_{i=1}^{N}\delta(\boldsymbol{r}-\hat{\boldsymbol{r}}_i) \end{equation}
这是个单粒子算符。电子位置$\hat{\boldsymbol{r}}_i$是算符,而变量$\boldsymbol{r}$自然不是。根据式(214)-二次量子化,其在Bloch表象中为:
\begin{equation} \label{eq:68} \hat{\rho}(\boldsymbol{r})=\sum_{\substack{\boldsymbol{k},\boldsymbol{k’}\\ \sigma,\sigma’}}\langle\boldsymbol{k}\sigma|\delta(\boldsymbol{r}-\hat{\boldsymbol{r}})|\boldsymbol{k’}\sigma’\rangle a_{\boldsymbol{k}\sigma}^\dagger a_{\boldsymbol{k’}\sigma’} \end{equation}
矩阵元作如下计算:
\[ \begin{split} \langle\boldsymbol{k}\sigma|\delta(\boldsymbol{r}-\hat{\boldsymbol{r}})|\boldsymbol{k’}\sigma’\rangle&=\sum_{\sigma^{\prime\prime}}\int\mathrm{d}^3r^{\prime\prime}\langle\boldsymbol{k}\sigma|\delta(\boldsymbol{r}-\hat{\boldsymbol{r}})|\boldsymbol{r^{\prime\prime}}\sigma^{\prime\prime}\rangle\langle\boldsymbol{r^{\prime\prime}}\sigma^{\prime\prime}|\boldsymbol{k’}\sigma’\rangle=\
&=\sum_{\sigma^{\prime\prime}}\int\mathrm{d}^3r^{\prime\prime}\delta(\boldsymbol{r}-\boldsymbol{r^{\prime\prime}})\langle\boldsymbol{k}\sigma|\boldsymbol{r^{\prime\prime}}\sigma^{\prime\prime}\rangle\langle\boldsymbol{r^{\prime\prime}}\sigma^{\prime\prime}|\boldsymbol{k’}\sigma’\rangle=\
&=\sum_{\sigma^{\prime\prime}}\delta_{\sigma\sigma^{\prime\prime}}\delta_{\sigma^{\prime\prime}\sigma’}\langle\boldsymbol{k}\sigma|\boldsymbol{r}\sigma\rangle\langle\boldsymbol{r}\sigma|\boldsymbol{k’}\sigma\rangle=\
&=\delta_{\sigma\sigma’}\psi_\boldsymbol{k}^*(\boldsymbol{r})\psi_\boldsymbol{k’}(\boldsymbol{r}) \end{split} \]
如果像凝胶模型中一样,将Bloch函数限定为平面波,便得到
\begin{equation} \label{eq:69} \langle\boldsymbol{k}\sigma|\delta(\boldsymbol{r}-\hat{\boldsymbol{r}})|\boldsymbol{k’}\sigma’\rangle=\delta_{\sigma\sigma’}\frac{1}{V}e^{i(\boldsymbol{k’}-\boldsymbol{k})\cdot\boldsymbol{r}} \end{equation}
按照\eqref{eq:68},这意味着:
\begin{equation} \label{eq:70} \hat{\rho}(\boldsymbol{r})=\frac{1}{V}\sum_{\boldsymbol{k},\boldsymbol{q},\sigma}a_{\boldsymbol{k}\sigma}^\dagger a_{\boldsymbol{k+q}\sigma}e^{i\boldsymbol{q}\cdot\boldsymbol{r}} \end{equation}
作傅里叶变换得到:
\begin{equation} \label{eq:71} \hat{\rho}_\boldsymbol{q}=\sum_{\boldsymbol{k},\sigma}a_{\boldsymbol{k}\sigma}^\dagger a_{\boldsymbol{k+q}\sigma} \end{equation}
可以看出:
\begin{equation} \label{eq:72} \hat{\rho}_\boldsymbol{q}^\dagger=\hat{\rho}_\boldsymbol{-q};\qquad\hat{\rho}_\boldsymbol{q=0}=\widehat{N} \end{equation}
稍加计算也能发现:
\[ \begin{split} \hat{\rho}_\boldsymbol{q}\hat{\rho}_\boldsymbol{-q}&=\sum_{\boldsymbol{k}\sigma}a_{\boldsymbol{k}\sigma}^\dagger a_{\boldsymbol{k+q}\sigma}\sum_{\boldsymbol{p}\sigma’}a_{\boldsymbol{p}\sigma’}^\dagger a_{\boldsymbol{p-q}\sigma’}=\
&=\sum_{\substack{\boldsymbol{k},\boldsymbol{p}\\ \sigma,\sigma’}}a_{\boldsymbol{k}\sigma}^\dagger a_{\boldsymbol{k+q}\sigma}a_{\boldsymbol{p}\sigma’}^\dagger a_{\boldsymbol{p-q}\sigma’}=\
&=\sum_{\substack{\boldsymbol{k},\boldsymbol{p}\\ \sigma,\sigma’}}a_{\boldsymbol{k}\sigma}^\dagger\left(\delta_{\boldsymbol{k+q},\boldsymbol{p}}\delta_{\sigma\sigma’}-a_{\boldsymbol{p}\sigma’}^\dagger a_{\boldsymbol{k+q}\sigma}\right)a_{\boldsymbol{p-q}\sigma’}=\
&=\sum_{\boldsymbol{k}\sigma}a_{\boldsymbol{k}\sigma}^\dagger a_{\boldsymbol{k}\sigma}-\sum_{\substack{\boldsymbol{k},\boldsymbol{p}\\ \sigma,\sigma’}}a_{\boldsymbol{p}\sigma’}^\dagger a_{\boldsymbol{k}\sigma}^\dagger a_{\boldsymbol{p-q}\sigma’}a_{\boldsymbol{k+q}\sigma}=\
&=\widehat{N}-\sum_{\substack{\boldsymbol{k},\boldsymbol{p}\\ \sigma,\sigma’}}a_{\boldsymbol{p}\sigma’}^\dagger\left(\delta_{\boldsymbol{k},\boldsymbol{p-q}}\delta_{\sigma\sigma’}-a_{\boldsymbol{p-q}\sigma’}a_{\boldsymbol{k}\sigma}^\dagger\right)a_{\boldsymbol{k+q}\sigma}=\
&=\widehat{N}-\sum_{\boldsymbol{p}\sigma}a_{\boldsymbol{p}\sigma}^\dagger a_{\boldsymbol{p}\sigma}+\sum_{\boldsymbol{p}\sigma’}a_{\boldsymbol{p}\sigma’}^\dagger a_{\boldsymbol{p-q}\sigma’}\sum_{\boldsymbol{k}\sigma}a_{\boldsymbol{k}\sigma}^\dagger a_{\boldsymbol{k+q}\sigma}=\
&=\hat{\rho}_\boldsymbol{-q}\hat{\rho}_\boldsymbol{q} \end{split} \]
即
\[ [\hat{\rho}_\boldsymbol{q},\hat{\rho}_\boldsymbol{-q}]=0 \]
据此可将凝胶模型的哈密顿量用密度算符表示,动能项不变:
\[ \begin{split} H_\text{ee}=&\frac{1}{2}\sum_{\substack{\boldsymbol{k},\boldsymbol{p},\boldsymbol{q}\\ \sigma,\sigma’}}^{q\neq0}v_0(\boldsymbol{q})a_{\boldsymbol{k}+\boldsymbol{q}\sigma}^\dagger a_{\boldsymbol{p}-\boldsymbol{q}\sigma’}^\dagger a_{\boldsymbol{p}\sigma’}a_{\boldsymbol{k}\sigma}=\
=&\frac{1}{2}\sum_{\substack{\boldsymbol{k},\boldsymbol{p},\boldsymbol{q}\\ \sigma,\sigma’}}^{q\neq0}v_0(\boldsymbol{q})a_{\boldsymbol{k}+\boldsymbol{q}\sigma}^\dagger\left(-\delta_{\sigma\sigma’}\delta_{\boldsymbol{k},\boldsymbol{p-q}}+a_{\boldsymbol{k}\sigma}a_{\boldsymbol{p-q}\sigma’}^\dagger\right)a_{\boldsymbol{p}\sigma’}=\
=&-\frac{1}{2}\sum_{\boldsymbol{q},\boldsymbol{p},\sigma}^{q\neq0}v_0(\boldsymbol{q})a_{\boldsymbol{p}\sigma}^\dagger a_{\boldsymbol{p}\sigma}+\frac{1}{2}\sum_{\boldsymbol{q}}^{q\neq0}v_0(\boldsymbol{q})\sum_{\boldsymbol{k},\sigma}a_{\boldsymbol{k}+\boldsymbol{q}\sigma}^\dagger a_{\boldsymbol{k}\sigma}\cdot\
&\cdot\sum_{\boldsymbol{p},\sigma’}a_{\boldsymbol{p-q}\sigma’}^\dagger a_{\boldsymbol{p}\sigma’} \end{split} \]
于是凝胶模型哈密顿量变成:
\begin{equation} \label{eq:73} H=\frac{1}{2}\sum_{\boldsymbol{k}\sigma}\varepsilon_0(\boldsymbol{k})a_{\boldsymbol{k}\sigma}^\dagger a_{\boldsymbol{k}\sigma}+\frac{1}{2}\sum_{\boldsymbol{q}}^{q\neq0}v_0(\boldsymbol{q})\left\{\hat{\rho}_\boldsymbol{q}^\dagger\hat{\rho}_\boldsymbol{q}-\widehat{N}\right\} \end{equation}
为了深入了解此模型的物理本质,现在计算它的基态能。我们采用一阶微扰论,根据变分原理它能给出基态能的上界。将库伦相互作用$H_\text{ee}$作为微扰;未扰系统便是(Sommerfeld模型):
\begin{equation} \label{eq:74} H_0=\frac{1}{2}\sum_{\boldsymbol{k}\sigma}\varepsilon_0(\boldsymbol{k})a_{\boldsymbol{k}\sigma}^\dagger a_{\boldsymbol{k}\sigma} \end{equation}
有精确解。在
"未扰"基态$|E\_0\rangle$
中$N$个电子占据了小于限制能$\varepsilon_F$的所有态,叫做费米能(Fermi energy):
\begin{equation} \label{eq:75} \varepsilon_0(\boldsymbol{k})a=\frac{\hbar^2k^2}{2m}\leq\varepsilon_F=\frac{\hbar^2k_F^2}{2m} \end{equation}
$k_F$叫做费米波矢(Fermi wavevector),可由如下计算得到:由于能量色散各向同性
\begin{equation} \label{eq:76} \varepsilon_0(\boldsymbol{k})=\varepsilon_0(k) \end{equation}
电子在$\boldsymbol{k}$空间占据半径为$k_F$的球体中所有态。由于周期性边界条件\eqref{eq:46}$\boldsymbol{k}$空间中的$\boldsymbol{k}$-点是离散的,每个$\boldsymbol{k}$-点可占据
\begin{equation} \label{eq:77} \text{网格体积}\qquad\Delta k=\frac{(2\pi)^3}{L^3}=\frac{(2\pi)^3}{V} \end{equation}
若是考虑自旋简并,便会得到电子数与费米波矢$k_F$之间的关系:
\[N=2\frac{1}{\Delta k}\left(\frac{4\pi}{3}k\_F^3\right)=\frac{V}{3\pi^2}k\_F^3\]即
\begin{gather} \label{eq:78} k_F=\left(3\pi^2\frac{N}{V}\right)^{1/3}\
\label{eq:79} \varepsilon_F=\frac{\hbar^2}{2m}\left(3\pi^2\frac{N}{V}\right)^{2/3} \end{gather}
每个粒子的平均能量$\bar{\varepsilon}$是:
\begin{equation} \label{eq:80} \bar{\varepsilon}=\frac{2}{N}\left(\int_{k\leq k_F}\mathrm{d}^3k\,\frac{\hbar^2k^2}{2m}\right)\frac{1}{\Delta k}=\frac{3}{5}\varepsilon_F \end{equation}
在热力学极限下上式用到了
\[ \sum_{\boldsymbol{k}}\to\frac{1}{\Delta \boldsymbol{k}}\int\mathrm{d}^3k \]
并考虑了自旋简并。于是得到基态能:
\begin{equation} \label{eq:81} E_0=N\bar{\varepsilon}=\frac{3}{5}N\varepsilon_F \end{equation}
现介绍几个标准缩写(standard abbreviations):
\begin{align} \label{eq:83} n_\text{e}&=\frac{N}{V}:\quad&\text{平均电子密度}\
v_\text{e}&=\frac{1}{n_\text{e}}:\quad&\text{平均电子体积}\
\end{align}
$v_\text{e}$由无量纲的密度参数(density parameter)$r_s$决定:
\begin{equation} \label{eq:84} v_\text{e}=\frac{4\pi}{3}(a_Br_s)^3 \end{equation}
其中
\begin{equation} \label{eq:85} a_B=\frac{4\pi\varepsilon_0\hbar^2}{me^2}=0.529\overset{\lower.5em\circ}{\mathrm{A}} \end{equation}
为玻尔半径(Bohr radius)。以类似的方式引入能量参数
\begin{equation} \label{eq:86} 1\,\textrm{ryd}=\frac{1}{4\pi\varepsilon_0}\frac{e^2}{2a_B}=13.605\,\textrm{eV} \end{equation}
那么费米能$\varepsilon_F$可表示成:
\begin{equation} \label{eq:87} \varepsilon_F=\frac{\alpha^2}{r_s^2}[\mathrm{ryd}];\quad\alpha=\left(\frac{9\pi}{4}\right)^{1/3} \end{equation}
未扰基态能便是:
\begin{equation} \label{eq:88} E_0=N\frac{2.21}{r_s^2}[\mathrm{ryd}] \end{equation}
现在加入微扰$H_\text{ee}$并计算一阶能量修正:
\begin{equation} \label{eq:89} \varepsilon^{(1)}=\frac{1}{2N}\sum_{\substack{\boldsymbol{k},\boldsymbol{p},\boldsymbol{q}\\ \sigma,\sigma’}}^{q\neq0}v_0(\boldsymbol{q})\Big\langle E_0\Big|a_{\boldsymbol{k}+\boldsymbol{q}\sigma}^\dagger a_{\boldsymbol{p}-\boldsymbol{q}\sigma’}^\dagger a_{\boldsymbol{p}\sigma’}a_{\boldsymbol{k}\sigma}\Big|E_0\Big\rangle \end{equation}
上式中的产生湮灭算符作用于$|E_0\rangle$后,还须产生$|E_0\rangle$,否则与左矢内积为零,即湮灭算符作用于费米球内的态,而后产生算符填充这些球内的空穴,故只有以下两项对微扰修正有贡献:
1)直接项(Direct Term):
\begin{equation} \label{eq:90} \boldsymbol{k}=\boldsymbol{k}+\boldsymbol{q};\quad\boldsymbol{p}=\boldsymbol{p}-\boldsymbol{q}\iff q=0 \end{equation}
基于之前的讨论,这种项不会在求和中出现!
2)交换项(Exchange Term):
\begin{equation} \label{eq:91} \sigma=\sigma’;\quad\boldsymbol{k}+\boldsymbol{q}=\boldsymbol{p};\quad\boldsymbol{p}-\boldsymbol{q}=\boldsymbol{k} \end{equation}
这是典型的量子力学的项,并没有经典对应。它来源于$N$-粒子态的反对称化原理:
\begin{align} \label{eq:92} \begin{split} \varepsilon^{(1)}&=\frac{1}{2N}\sum_{\boldsymbol{k},\boldsymbol{q},\sigma}^{q\neq0}v_0(\boldsymbol{q})\Big\langle E_0\Big|a_{\boldsymbol{k}+\boldsymbol{q}\sigma}^\dagger a_{\boldsymbol{p}-\boldsymbol{q}\sigma’}^\dagger a_{\boldsymbol{p}\sigma’}a_{\boldsymbol{k}\sigma}\Big|E_0\Big\rangle=\
&=-\frac{1}{2N}\sum_{\boldsymbol{k},\boldsymbol{q},\sigma}^{q\neq0}v_0(\boldsymbol{q})\Big\langle E_0\Big|\hat{n}_{\boldsymbol{k}+\boldsymbol{q}\sigma} \hat{n}_{\boldsymbol{k}\sigma}\Big|E_0\Big\rangle \end{split} \end{align}
由于在未扰基态$|E_0\rangle$,费米球内的所有态都被占据而球外都没被占据,便有:
\begin{equation} \label{eq:93} \varepsilon^{(1)}=-\frac{1}{2N}\sum_{\boldsymbol{k},\boldsymbol{q},\sigma}^{q\neq0}v_0(\boldsymbol{q})\varTheta(k_F-|\boldsymbol{k}+\boldsymbol{q}|)\varTheta(k_F-k) \end{equation}
在对自旋求和之后,将求和变积分:
\[ \varepsilon^{(1)}=-\frac{V}{N}\frac{e^2}{\varepsilon_0(2\pi)^6}\int\mathrm{d}^3k\int\mathrm{d}^3q\,\frac{1}{q^2}\varTheta(k_F-|\boldsymbol{k}+\boldsymbol{q}|)\varTheta(k_F-k) \]
做替换
\[ \boldsymbol{k}\Rightarrow\boldsymbol{x}=\boldsymbol{k}+\frac{1}{2}\boldsymbol{q} \]
便得到
\begin{align} \label{eq:94} \varepsilon^{(1)}&=-\frac{V}{N}\frac{e^2}{\varepsilon_0(2\pi)^6}\int\mathrm{d}^3q\,\frac{1}{q^2}2S(q)\
\label{eq:95} S(q)&=\frac{1}{2}\int\mathrm{d}^3x\,\varTheta\left(k_F-\left|\boldsymbol{x}+\frac{1}{2}\boldsymbol{q}\right|\right)\varTheta\left(k_F-\left|\boldsymbol{x}-\frac{1}{2}\boldsymbol{q}\right|\right) \end{align}
由图 3中的球缺(spherical segment)示意图易得:
\begin{equation} \label{eq:96} S(q)=\varTheta\left(k_F-\frac{1}{2}q\right)\left\{k_F^3-\frac{3}{4}qk_F^2+\frac{1}{16}q^3\right\} \end{equation}
此处用到球缺的体积公式:
\[ S= \pi \times h^2\times(R-\frac{h}{3})= \pi \times h \times\frac{3r^2+h^2}{6} \]
这里$R$是球体的半径,$h$是球缺的高,$r$是底面半径。再代入\eqref{eq:94}中即可得到:
\[ \varepsilon^{(1)}=-\frac{0.916}{r_s}[\mathrm{ryd}] \]
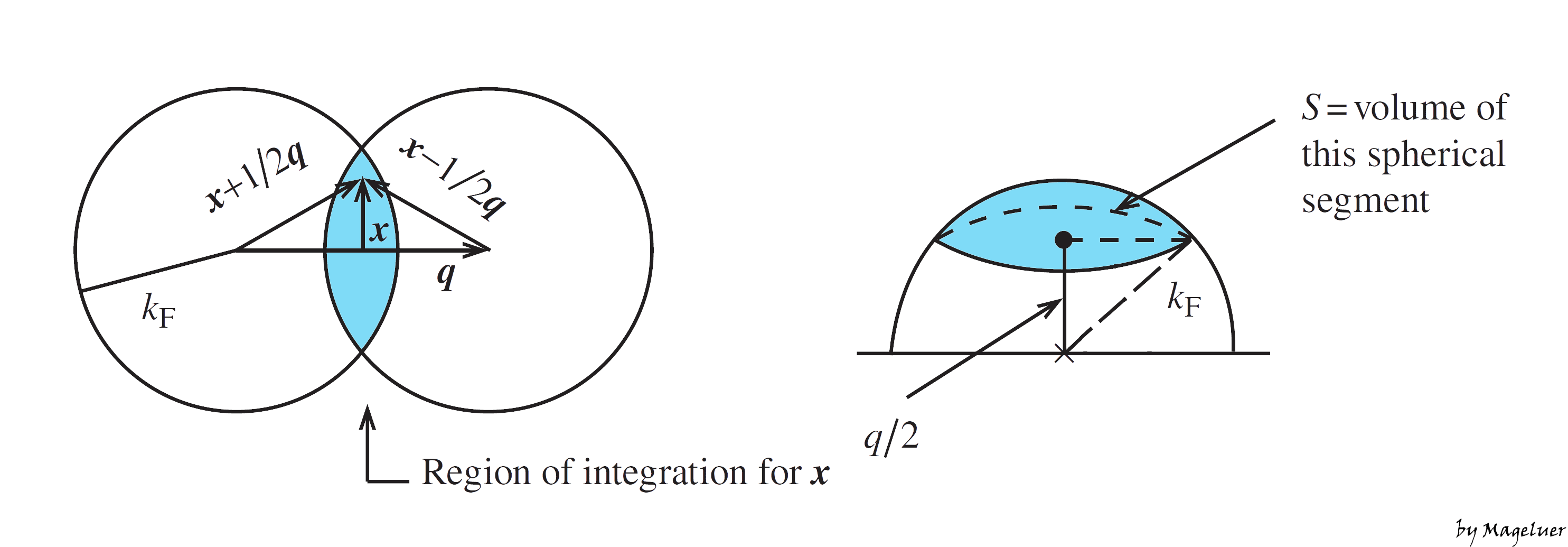
最终得到单粒子的基态能:
\begin{equation} \label{eq:97} \frac{1}{N}E_\text{min}[\mathrm{ryd}]=\frac{2.21}{r_s^2}-\frac{0.916}{r_s}+\varepsilon_\text{corr}=\varepsilon \end{equation}
第一项是动能\eqref{eq:88},第二项即所谓交换能(exchange energy)。后者为全同粒子系统的典型特征,也是不可分辨性原理的直接结果,对于费米子来说就是泡利不相容原理。它保证自旋相同的电子不会靠得太近。所有使相同电荷的粒子保持一定距离的效应都会降低其基态能。这也是\eqref{eq:97}中负号的来源,相当于一种引力,当$r_s$取适当值时,系统处于束缚态。最后一项叫做关联能(correlation energy)。它给出微扰论所得能量与精确结果之间的误差,因此自然是未知的。现代多体理论方法给出如下展开式:
\begin{equation} \label{eq:98} \varepsilon_\text{corr}=\frac{2}{\pi^2}(1-\ln2)\ln r_s-0.094+O(r_s\ln r_s)[\mathrm{ryd}] \end{equation}
这样一个简单的凝胶模型已经给出了有用的结果,比如,$\varepsilon-\varepsilon_\text{corr}$在
\[ \begin{split} r_0=(r_s)_\text{min}&=4.83,\
(\varepsilon-\varepsilon_\text{corr})_\text{min}&=-0.095[\mathrm{ryd}]=-1.29[\mathrm{eV}] \end{split} \]
这意味着电子密度的最优值,对应着最佳离子间距,并至少是定性地解释了金属键(metallic bonding)。
1.3 Hubbard模型
凝胶模型的简化关键在于其忽略了晶格结构,将离子视作均匀分布的正电荷背景。于是Bloch函数成了平面波\eqref{eq:45},在整个晶体中电子的占有几率是个常数。胶体模型从一开始就只限于宽能带电子,比如碱金属的导带电子。
对于窄能带电子,其迁移率相对较低,其在晶格离子处的占有几率与宽能带电子大不一样。平面波自然不再适用于这种能带结构的电子。一个好得多的出发点是所谓紧束缚近似(tight-binding approximation)。紧束缚近似适用于这类情况:原子波函数之间的重叠足够大以至于需要对独立原子的构象进行修正,但还没有大到完全与原子波函数的描述无关。它最适用于过渡金属半填满的$d$-壳层以及描述绝缘体的电子结构。
假定晶格势$\widehat{V}(\boldsymbol{r})$很强且带电子的迁移率很低,在格点附近,原子哈密顿量
\begin{equation} \label{eq:99} H_\text{at}=\sum_{i=1}^{N_\text{i}}h_\text{at}^{(i)} \end{equation}
是独立原子的哈密顿量之和,应当是整个周期性晶格哈密顿量的不错的近似,它和$H_0$\eqref{eq:7}非常相似:
\begin{equation} \label{eq:100} h_\text{at}^{(i)}\varphi_n(\boldsymbol{r}-\boldsymbol{R}_i)=\varepsilon_n\varphi_n(\boldsymbol{r}-\boldsymbol{R}_i) \end{equation}
这里$\varphi_n$是原子波函数,视为已知。指数$n$象征一组量子数。其次假定$\varphi_n$非常局域化,超过“一定范围”就变得非常小。集中于$\boldsymbol{R}_i$,$\boldsymbol{R}_j$处的波函数之间重叠非常小,这源于不同原子间电子的隧穿几率很小,原子能级劈裂很小,即窄能带。
在极端情况下,晶体哈密顿量只有在超过一定范围(此时原子波函数为零)才和$H_\text{at}$产生差别,于是$\varphi_n$便是整个哈密顿量定态波函数很好的近似。
对于无相互作用的电子哈密顿量\eqref{eq:7},
\begin{equation} \label{eq:101} H_0=\sum_{i=1}^{N_\text{e}}h_0^{(i)} \end{equation}
为了计算对于极端情况的修正,采用如下晶格哈密顿量:
\begin{equation} \label{eq:102} h_0=h_\text{at}+V_1(\boldsymbol{r}) \end{equation}
这里$V_1(\boldsymbol{r})$包含了由原子周期势产生真实晶体周期势所需的所有修正。 如果$\varphi_n$满足薛定谔方程\eqref{eq:100},它必然也满足
\begin{equation} \label{eq:103} h_0\psi_{n\boldsymbol{k}}(\boldsymbol{r})=\varepsilon_n(\boldsymbol{k})\psi_{n\boldsymbol{k}}(\boldsymbol{r}) \end{equation}
前提是,任何$\varphi_n(\boldsymbol{r})$存在的地方$V_1(\boldsymbol{r})$都消失。若果是这种情况,每个原子能级$\varphi_n(\boldsymbol{r})$在周期势中都会贡献$N_\text{i}$个能级,对$N_\text{i}$个晶格$\boldsymbol{R}_i$中的每一个都会有波函数$\varphi_n(\boldsymbol{r}-\boldsymbol{R}_i)$。在满足Bloch定理\eqref{eq:15}的条件下,这$N_\text{i}$个简并波函数的线性组合成试探Bloch函数解
\begin{equation} \label{eq:104} \psi_{n\boldsymbol{k}}(\boldsymbol{r})=\frac{1}{\sqrt{N_\text{i}}}\sum_{j=1}^{N_\text{i}}e^{i\boldsymbol{k}\cdot\boldsymbol{R}_j}\varphi_n(\boldsymbol{r}-\boldsymbol{R}_j) \end{equation}
此函数保留了原子能级的特征。这种方法得到的能带没什么结构,$\varepsilon_n(\boldsymbol{k})$仅仅是简单的原子能级$\varepsilon_n$,与$\boldsymbol{k}$的取值无关。为了弥补这种不足,更实际的假设应当是:在$V_1(\boldsymbol{r})$变得相当可观之前,$\varphi_n(\boldsymbol{r})$变小,但没完全消失。这启示我们寻找一个满足整个晶体的薛定谔方程的解,其形式仍然符合\eqref{eq:104}:
\[ \psi(\boldsymbol{r})=\frac{1}{\sqrt{N_\text{i}}}\sum_{j=1}^{N_\text{i}}e^{i\boldsymbol{k}\cdot\boldsymbol{R}_j}\phi(\boldsymbol{r}-\boldsymbol{R}_j) \]
这里$\phi(\boldsymbol{r})$不一定正好是一个定态原子波函数,它需要由后续计算确定。如果乘积$V_1(\boldsymbol{r})\varphi_n(\boldsymbol{r})$虽然不为零,但也足够小,有理由期望$\phi(\boldsymbol{r})$与原子波函数$\varphi_n(\boldsymbol{r})$或者与$\varphi_n(\boldsymbol{r})$简并的波函数非常接近。基于此,$\phi(\boldsymbol{r})$可由少数几个局域原子波函数的线性展出:
\[ \phi(\boldsymbol{r})=\sum_n b_n\varphi_n(\boldsymbol{r}) \]
附注:
- 我们的第一次严格近似是只包含局域的(即束缚的)原子波函数。一组完整的原子能级应当包含电离了的原子。这也是该方法不能用于近自由电子能级的原因。
- 因为这种对$\phi(\boldsymbol{r})$近似方式,紧束缚近似有时也被称作原子轨道线性组合法(linear combination of atomic orbits)(或LCAO)。
对比\eqref{eq:29}可见,我们把精确的Wannier函数替换成了束缚的原子波函数的组合。用$\varphi_m^*(\boldsymbol{r})$乘\eqref{eq:103}并对$\boldsymbol{r}$积分可得:
\[ \int\mathrm{d}\boldsymbol{r}\,\varphi_m^*(\boldsymbol{r})h_0\psi(\boldsymbol{r})=\int\mathrm{d}\boldsymbol{r}\,\varphi_m^*(\boldsymbol{r})\left(h_\text{at}+V_1(\boldsymbol{r})\right)\psi(\boldsymbol{r})=\varepsilon(\boldsymbol{k})\int\mathrm{d}\boldsymbol{r}\,\varphi_m^*(\boldsymbol{r})\psi(\boldsymbol{r}) \]
再有:
\[ \int\mathrm{d}\boldsymbol{r}\,\varphi_m^*(\boldsymbol{r})h_\text{at}\psi(\boldsymbol{r})=\int\mathrm{d}\boldsymbol{r}\,\left(h_\text{at}\varphi_m(\boldsymbol{r})\right)^*\psi(\boldsymbol{r})=\varepsilon_m\int\mathrm{d}\boldsymbol{r}\,\varphi_m^*(\boldsymbol{r})\psi(\boldsymbol{r}) \]
于是得到:
\[ (\varepsilon(\boldsymbol{k})-\varepsilon_m)\int\mathrm{d}\boldsymbol{r}\,\varphi_m^*(\boldsymbol{r})\psi(\boldsymbol{r})=\int\mathrm{d}\boldsymbol{r}\,\varphi_m^*(\boldsymbol{r})V_1(\boldsymbol{r})\psi(\boldsymbol{r}) \]
将$\psi(\boldsymbol{r})$展开式代入上式,并利用原子波函数的正交性:
\[ \int\mathrm{d}\boldsymbol{r}\,\varphi_m^*(\boldsymbol{r})\varphi_n(\boldsymbol{r})=\delta_{mn} \]
最终得到如下本征方程,解此方程可得到系数$b_n(\boldsymbol{k})$和Bloch能$\varepsilon(\boldsymbol{k})$:
\begin{equation} \begin{split} (\varepsilon(\boldsymbol{k})-\varepsilon_m)b_m=&-(\varepsilon(\boldsymbol{k})-\varepsilon_m)\sum_n\left(\sum_{\boldsymbol{R}\neq0}\int\mathrm{d}\boldsymbol{r}\,\varphi_m^*(\boldsymbol{r})\varphi_n(\boldsymbol{r-R})e^{i\boldsymbol{k}\cdot\boldsymbol{R}}\right)b_n+\
&+\sum_n\left(\int\mathrm{d}\boldsymbol{r}\,\varphi_m^*(\boldsymbol{r})V_1(\boldsymbol{r})\varphi_n(\boldsymbol{r})\right)b_n+\
&+\sum_n\left(\sum_{\boldsymbol{R}\neq0}\int\mathrm{d}\boldsymbol{r}\,\varphi_m^*(\boldsymbol{r})V_1(\boldsymbol{r})\varphi_n(\boldsymbol{r-R})e^{i\boldsymbol{k}\cdot\boldsymbol{R}})\right)b_n \end{split} \label{eq:105} \end{equation}
上式右边第一项包含此种形式的积分:
\[ \int\mathrm{d}\boldsymbol{r}\,\varphi_m^*(\boldsymbol{r})\varphi_n(\boldsymbol{r-R}) \]
我们对于原子能级非常定域化的假设意味着该项非常小。
附注:
积分中包含对两个不同格点波函数的乘积的积分叫做重叠积分(overlap integrals)。紧束缚近似利用了重叠积分很小这一特性。该积分在磁性理论中也发挥重要作用。
\eqref{eq:105}第三项也很小,因为它也包含了重叠积分。最后,我们认为\eqref{eq:105}第二项很小因为我们期望当周期势偏离原子势时离格点已经足够远,而这时原子波函数已变得很小。
附注:
相比其他假设这个假设有点站不住脚,因为离子势衰减速度无需和原子波函数一样快。但是,这对最终结果并无致命影响,因为问题中该项并不依赖于$\boldsymbol{k}$。在某种意义上,该项的作用是修正元胞内的原子势以包含元胞外的离子场的影响;通过合理定义“原子”哈密顿量和能级,这一项也能变得和其他两项一样小。
最终发现\eqref{eq:105}右边(也即$(\varepsilon(\boldsymbol{k})-\varepsilon_m)$)总是很小。这意味着每当$b_m$不小的时候,$\varepsilon(\boldsymbol{k})-\varepsilon_m$一定很小(反之亦然)。故$\varepsilon(\boldsymbol{k})$必须接近某个原子能级,比如$\varepsilon_0$,所有的$b_m$除了那些相应的能级能量与其简并(或非常接近)的都必须很小:
\[ \varepsilon(\boldsymbol{k})\approx\varepsilon_0,\quad b_m\approx0\text{ unless }\varepsilon_m\approx\varepsilon_0 \]
如果上式为严格的等式,我们又会回到极端情况,晶体能级与原子能级相同。利用上式,我们可以将\eqref{eq:105}右侧求和指标$n$限定于那些能级能量与$\varepsilon_0$简并或者非常接近的几个,\eqref{eq:105}便成了一个分块对角矩阵方程。如果原子能级$0$是非简并的,即$s$能级(这里没有考虑SOC,只关注能级的轨道部分,自旋可通过在轨道波函数乘以相应自旋波函数引入,这样轨道能级简并度翻倍),在此近似下\eqref{eq:105}简化为由$s$能级(一般叫做“$s$带”)产生的能带能量的明确表达式。如果考虑$p$能级,它是三重简并的,\eqref{eq:105}便成为一组三个方程。同理,考虑$d$能级,就要解$5\times5$的矩阵方程。
如果解得的$\varepsilon(\boldsymbol{k})$在某些$\boldsymbol{k}$处离所考虑的原子能级足够远,那么就要重复以上步骤,将此时$\varepsilon(\boldsymbol{k})$所接近的能级也包括进$\phi$的展开式。实际上,在算过渡金属能带时常常要解包含了$s$-和$d$-能级的$6\times6$的方程,其原子态含有外层$s$-壳层及部分填充的$d$-壳层。此过程即所谓“$s$-$d$混合”或“杂化”。
通常原子波函数短程有效,\eqref{eq:105}中对$\boldsymbol{R}$的求和仅需保留近邻项,这对后续分析又大大简化。下面就举个最简单的$s$能级的例子。
如果\eqref{eq:105}中除了单个$s$能级的系数$b$剩下的全为零,便直接得到其相应$s$-带能带结构:
\begin{equation} \label{eq:106} \varepsilon_n(\boldsymbol{k})=\varepsilon_n+\frac{v_n+\sum_j^{\neq0}\gamma_n^{(j)}e^{i\boldsymbol{k}\cdot\boldsymbol{R}_j}}{1+\sum_j^{\neq0}\alpha_n^{(j)}e^{i\boldsymbol{k}\cdot\boldsymbol{R}_j}} \end{equation}
这里$\varepsilon_n=\varepsilon_s$为$s$-能级能量,并且
\begin{align} \label{eq:107} v_n&=\int\mathrm{d}\boldsymbol{r}\,V_1(\boldsymbol{r})|\varphi_n(\boldsymbol{r})|^2\
\label{eq:108} T_0^{(n)}&=\varepsilon_n+v_n\
\label{eq:109} \alpha_n^{(j)}&=\int\mathrm{d}\boldsymbol{r}\,\varphi_n^*(\boldsymbol{r})\varphi_n(\boldsymbol{r}-\boldsymbol{R}_j)\
\label{eq:110} \gamma_n^{(j)}&=\int\mathrm{d}\boldsymbol{r}\,\varphi_n^*(\boldsymbol{r})V_1(\boldsymbol{r})\varphi_n(\boldsymbol{r}-\boldsymbol{R}_j) \end{align}
上面这些系数可据对称性进行简化。由于$\varphi_n$为$s$-能级,它是实数且仅依赖于$r$的大小。由此可得$\alpha_n(-\boldsymbol{R})=\alpha_n(\boldsymbol{R})$。此外由于Bravais格子的空间反演对称性要求$V_1(-\boldsymbol{R})=V_1(\boldsymbol{R})$,便有$\gamma_n(-\boldsymbol{R})=\gamma_n(\boldsymbol{R})$。\eqref{eq:106}分母上的$\alpha$对分子的修正很小,故将其忽略。最后假设只有近邻重叠积分才有效,便得到最终简化形式:
\begin{equation} \label{eq:111} \varepsilon_n(\boldsymbol{k})=T_0^{(n)}+\sum_\Delta \gamma_n^{(1)}e^{i\boldsymbol{k}\cdot\boldsymbol{R}_\Delta} \end{equation}
其中$\Delta$表示坐标原点处原子的最近邻的原子。现在考虑一个简单立方晶格:
\begin{equation} \begin{gathered} \boldsymbol{R}_\Delta=a(\pm1,0,0),\quad a(0,\pm1,0)\quad a(0,0,\pm1)\
\varepsilon_n^\text{s.c.}(\boldsymbol{k})=T_0^{(n)}+2\gamma_n^{(1)}\left(\cos(k_xa)+\cos(k_ya)+\cos(k_za\right) \end{gathered} \label{eq:112} \end{equation}
这里$a$是晶格常数,$T_0^{(n)}$和$\gamma_n^{(1)}$是可由实验测定的参数。由对称性可知$\gamma_n^{(1)}$为常数,其表达式为
\[ \gamma_n^{(1)}=\int\mathrm{d}\boldsymbol{r}\,\varphi_n^*(x,y,z)V_1(x,y,z)\varphi_n(x-a,y,z) \]
可由带宽$W$确定:
\begin{equation} \label{eq:113} W_n^\text{s.c.}=12|\gamma_n^{(1)}| \end{equation}
由于带宽和重叠积分$\gamma$成正比,故紧束缚能带是窄带,能带间重叠越小,带宽越小。当能带重叠消失,带宽也消失,能带变成$N$重简并,和之前讨论的极限情况一致,那时电子束缚于$N$个独立的原子处。如图 4所示。

除此之外\eqref{eq:112}所反映的简单立方晶格的能带特征也是紧束缚近似的一般特征。比如:
- 当$ka$很小时,利用$\lim_{x\to0}\cos x\sim1-\frac{1}{2}x^2$,\eqref{eq:112}成为
\[ \varepsilon_n^\text{s.c.}(\boldsymbol{k})=T_0^{(n)}+6\gamma_n^{(1)}-\gamma_n^{(1)}k^2a^2 \] 与$\boldsymbol{k}$方向无关,即$\boldsymbol{k}=0$附近的等能面是个球面(这一特征可以推广到所有立方晶格的非简并能带)。带底在小$k$值附近是抛物线色散,这一点在凝胶模型中也适用。 - 沿着任何一条垂直于第一布里渊区正方形表面所绘的$\varepsilon$色散曲线,在穿过该面时斜率为零。例如,沿着$k_x$方向(此时$k_y$和$k_z$为常数),有
\[ \left.\frac{\partial}{\partial k_x}\varepsilon_n^\text{s.c.}(\boldsymbol{k})\right|_{k_x=\frac{\pi}{a}}=\left.-2a\gamma_n^{(1)}\sin(k_xa)\right|_{k_x=\frac{\pi}{a}}=0 \]
严格来讲\eqref{eq:111}仅适用于$s$-带,对于$p$-,$d$-,$f$-……能带需要考虑更多的简并度,但这里我们点到为止,就不展开讲了。接下来的处理限制在$s$-带,顺便把$n$指标也去掉。
在二次量子化形式下,$H_0$形如\eqref{eq:33}:
\begin{equation} \label{eq:114} H_0=\sum_{ij\sigma}T_{ij}a_{i\sigma}^\dagger a_{j\sigma} \end{equation}
紧束缚近似仅允许电子通过最近邻格点间的跃迁积分进行跃迁:
\begin{equation} \label{eq:115} T_{ij}=\frac{1}{N_\text{i}}\sum_\boldsymbol{k}\varepsilon(\boldsymbol{k})e^{i\boldsymbol{k}\cdot(\boldsymbol{R}_i-\boldsymbol{R}_j)} \end{equation}
带电子间的库伦相互作用\eqref{eq:56}自然仍然适用。转化到实空间便是
\begin{equation} \label{eq:116} H_\text{ee}=\frac{1}{2}\sum_{\substack{ijkl\\ \sigma,\sigma’}}v(ij;kl)a_{i\sigma}^\dagger a_{j\sigma’}^\dagger a_{l\sigma’}a_{k\sigma} \end{equation}
矩阵元通过原子波函数计算:
\begin{equation} \label{eq:117} v(ij;kl)=\frac{e^2}{4\pi\varepsilon_0}\iint\mathrm{d}^3r_1\,\mathrm{d}^3r_2\,\frac{\varphi^*(\boldsymbol{r}_1-\boldsymbol{R}_i)\varphi^*(\boldsymbol{r}_2-\boldsymbol{R}_j)\varphi(\boldsymbol{r}_2-\boldsymbol{R}_l)\varphi(\boldsymbol{r}_1-\boldsymbol{R}_k)}{|\boldsymbol{r}_1-\boldsymbol{r}_2|} \end{equation}
由于不同格点原子波函数的重叠积分很小,原子内的矩阵元
\begin{equation} \label{eq:118} U=v(ii;ii) \end{equation}
起主导作用。Hubbard就建议干脆就把电子-电子相互作用限定在这一项:
Hubbard模型:
\begin{equation} \label{eq:119} H=\sum_{ij\sigma}T_{ij}a_{i\sigma}^\dagger a_{j\sigma}+\frac{1}{2}U\sum_{i,\sigma}\hat{n}_{i\sigma}\hat{n}_{i-\sigma} \end{equation}
(注意:$\sigma=\uparrow(\downarrow)\iff-\sigma=\downarrow(\uparrow)$)。Hubbard模型必定是能让我们同时研究动能相互作用,库伦相互作用,泡利不相容原理以及晶格结构的最简单的模型,可谓小巧精悍。
为得到\eqref{eq:119}而用的大幅简化当然也给模型的使用带来局限性:
该模型用来讨论:
- 窄能带固体的电子性质(例如,过渡金属),
- 能带磁性,
- 金属-绝缘体转变(“Mott转变”),
- 统计力学的一般性原理,
- 高温超导。
虽然结构简单,但Hubbard模型目前还没有精确解,还得借助各种近似来求解。接下来的部分用一些例子来讨论。